Dreiecksverteilung

Die Dreiecksverteilung (oder Simpsonverteilung, nach Thomas Simpson) ist eine stetige Wahrscheinlichkeitsverteilung, die in der Wahrscheinlichkeitstheorie und Statistik verwendet wird.

Definition

Die Dreiecksverteilung ist definiert durch die auf dem Intervall ${\displaystyle \left[a,b\right]}$ definierte Wahrscheinlichkeitsdichtefunktion

${\displaystyle f(x)={\begin{cases}{\frac {2(x-a)}{(b-a)(c-a)}},&{\text{wenn }}a\leq x$

Hierbei bestimmen die Parameter ${\displaystyle a}$ (minimaler Wert), ${\displaystyle b}$ (maximaler Wert) und ${\displaystyle c}$ (wahrscheinlichster Wert) die Gestalt der Dreiecksverteilung (${\displaystyle a$ und ${\displaystyle a\leq c\leq b}$). Der Graph der Dichtefunktion sieht wie ein Dreieck aus und gibt dieser Verteilung ihren Namen. Die ${\displaystyle y}$-Achse zeigt die Dichte der jeweiligen Wahrscheinlichkeit für einen Wert ${\displaystyle x\in \left[a,b\right]}$.

Eigenschaften

Verteilungsfunktion

Die Verteilungsfunktion ist

${\displaystyle F(x)={\begin{cases}{\frac {(x-a)^{2}}{(b-a)(c-a)}},&{\text{wenn }}a\leq x$

Die Umkehrfunktion der Verteilungsfunktion lautet

${\displaystyle F^{-1}(y)={\begin{cases}a {\sqrt {y(b-a)(c-a)}},&{\text{wenn }}0\leq y\leq {\frac {(c-a)}{(b-a)}}\\b-{\sqrt {(b-a)(b-c)}}{\sqrt {(1-y)}},&{\text{wenn }}{\frac {(c-a)}{(b-a)}}\leq y\leq 1\end{cases}}}$

Erwartungswert und Median

Der Erwartungswert einer dreiecksverteilten Zufallsvariable ${\displaystyle X}$ ist

${\displaystyle \operatorname {E} (X)={\frac {a b c}{3}}.}$

Für ${\displaystyle b-c>c-a}$ ist der Median ${\displaystyle m}$ gegeben durch

${\displaystyle m=b-{\sqrt {(b-a)(b-c)/2}}}$. Für diesen Fall ist der Median kleiner als der Erwartungswert; d. h. die Verteilung ist rechtsschief im Sinne von Pearson.

Varianz

Die Varianz einer dreiecksverteilten Zufallsvariable ${\displaystyle X}$ ergibt sich zu

${\displaystyle \operatorname {Var} (X)={\frac {a^{2} b^{2} c^{2}-ab-ac-bc}{18}}={\frac {(a-b)^{2} (b-c)^{2} (a-c)^{2}}{36}}.}$

Beziehung zu anderen Verteilungen

Summe gleichverteilter Zufallsgrößen

Die Summe zweier identischer unabhängiger und stetig gleichverteilter Zufallsvariablen ist dreiecksverteilt mit ${\displaystyle b-c=c-a}$, Standardabweichung ${\displaystyle {\sqrt {6}}(b-a)/12\approx 0{,}204(b-a)}$, mittlerer absoluter Abweichung ${\displaystyle (b-a)/6\approx 0{,}167(b-a)}$ und Interquartilsabstand ${\displaystyle (1-{\sqrt {2}}/2)(b-a)\approx 0{,}293(b-a)}$.

Betrag der Differenz gleichverteilter Zufallsgrößen

Der Betrag der Differenz zweier identischer unabhängiger und stetig gleichverteilter Zufallsvariablen ${\displaystyle |X_{1}-X_{2}|}$ ist dreiecksverteilt mit ${\displaystyle a=c=0}$.

Trapezverteilung

Die Dreiecksverteilung ist ein Spezialfall der Trapezverteilung.

Diskrete Dreiecksverteilung

Die stetige Dreiecksverteilung kann als Grenzwert einer diskreten Dreiecksverteilung aufgefasst werden.

Literatur

• Norman L. Johnson, Samuel Kotz: Non-Smooth Sailing or Triangular Distributions Revisited after Some 50 Years. In: The Statistician, Vol. 48, No. 2 (1999), S. 179–187

Weblinks

• Eric W. Weisstein: Triangular Distribution. In: MathWorld (englisch).
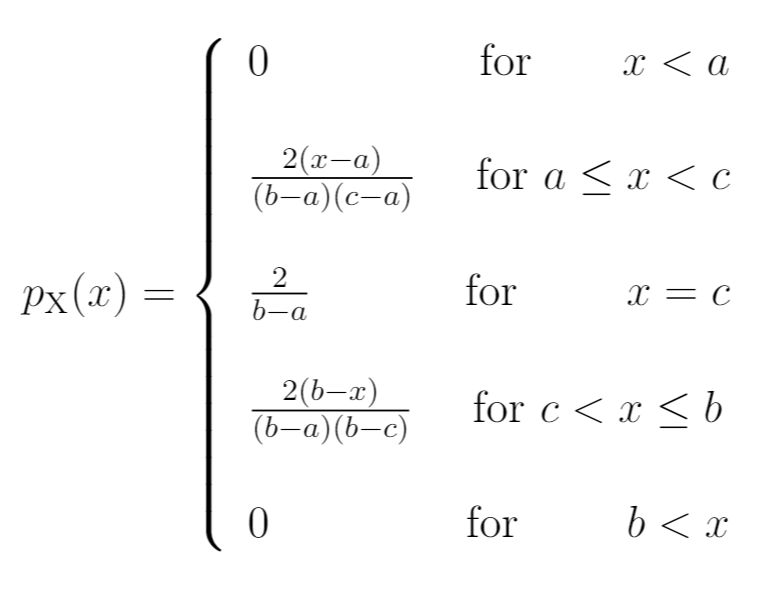